| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 코드스쿼드 마스터즈
- 2021.01.17
- 2021.01.11
- 백준
- 쉽게 배우는 운영체제
- 백준 9093
- 마스터즈 2주차 회고
- 2021.01.22
- 잃어버린 괄호
- 알고리즘
- 박재성
- java
- 알고리즘데이
- baekjoon1541
- 2020.01.08
- SWEA
- 2021.01.19
- 2021.01.06
- 2021.01.12
- 2021.01.18
- spring-boot
- 2021.01.21
- 백준 1149
- 코드스쿼드
- 자바
- algorithm
- 2021.01.14
- 괄호
- Til
- 2021.01.13
- Today
- Total
Cooper's devlog
Z : 1074 - JAVA 본문
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. 만약, N > 1이 라서
www.acmicpc.net
이번 문제는 Z라는 문제를 풀어보았다. 이전에는 이 문제를 해결하지 못해 다른 블로그를 참고해서 문제를 풀었었다.
그리고 한동안 나는 이 문제를 알고 있다고 생각했지만 다시 풀려고 하다보니 계속해서 빗발치는 틀렸습니다를 확인하였다;;
그래서 이번에 문제를 직접 풀어보고 다시 한번 로직을 정리하고자 글을 작성한다.
확실히 내가 직접 고민해보지 않으면 소용이 없는 것 같다.
[1. 간략한 분할정복 설명]
여기서 핵심을은 충분히 쪼개야 한다는 점이다. 충분히 쪼개지 않으면 결국에는 선형탐색과 같은 시간 복잡도를 가질 수도 있기 때문이다.
[2. 분할정복 사용법]
1. 문제 사례를 하나 이상의 작은 사례로 분할한다.
2. 작은 사례들을 각각 정복(conquer)한다. 작은 사례가 충분히 작지 않다면, 재귀함수를 통해 사례를 쪼갠다.
3. 만약 작은 사례에서 해당을 찾았다면 통합하여 원래 사례의 해답을 구한다.
[3. 접근 방법]
1. 간단한 Z 만들기
처음 문제를 접근할 때, 단순하게 생각하도록 노력했다. 우선적으로 문제의 이동 순서는 Z형태를 띄고 있다.
그러기 때문에 우선적으로 Z형태를 구현하는 것에 초점을 맞췄다.

위 그림은 행과 열의 이동 방향에 따라서 변화하는 행렬을 표시한 것이다. 그렇다면 위와 같은 모형으로 구현하기 위해서는 어떻게 해야 하는걸까?
public class Z_basic {
public static void main(String[] args) {
int[] dx = {0, 1, 0, 1};
int[] dy = {0, 0, 1, 1};
int x = 0; //기준 행
int y = 0; //기준 열
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
System.out.printf("행: %d, 열: %d \n", nx, ny);
}
}
}

위와 같이 행,열에 대한 움직임에 대한 배열을 선언 후, 반복문을 통해 순회하면 위와 같은 코드인 것을 확인할 수 있다.
2. Z 속에 Z 만들기
그 다음 단계는 문제에서 제시하는 것과 같이 Z 속에 Z를 한번 만들어보도록 하겠다. Z 속에 Z를 만드는 방법은 재귀함수를 사용하면 가능하다. 우선 아래와 같이 순회하는 형태를 그림으로 확인해보자.
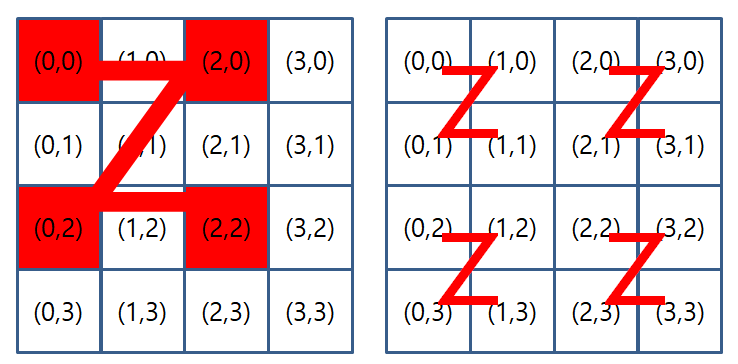
Z 속에 Z를 만드는 방법은 다음과 같다.
- 우선적으로 큰 Z를 방문한다.
- 내부의 Z는 재귀함수를 통해서 Z를 그리도록 한다.
이해가 되지 않는다면 아래 코드와 결과를 한번 확인해보자.
class Z_Intemediate {
static int arrSize = 4; ////배열의 크기
static int[] dx = {0, 1, 0, 1};
static int[] dy = {0, 0, 1, 1};
public static void main(String[] args) {
int x = 0; //시작 행
int y = 0; //시작 열
makeInnerZ(x, y, arrSize);
}
private static void makeInnerZ(int x, int y, int size) {
//큰 Z를 방문 확인 조건문
//해당 위치를 방문 후, 내부 Z를 만들어낸다.
if (size == 2) {
System.out.printf("Outer Z : 행: %d, 열: %d \n", x, y);
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
System.out.printf("Inner Z : 행: %d, 열: %d \n", nx, ny);
}
System.out.println();
return;
}
int newSize = size / 2;
//2. 내부 Z를 만들기 위한 내부 Z
makeInnerZ(x, y, newSize);
makeInnerZ(x, y + newSize, newSize);
makeInnerZ(x + newSize, y, newSize);
makeInnerZ(x + newSize, y + newSize, newSize);
}
}

1. 사이즈가 4인 배열은 재귀함수를 통해 내부를 탐색합니다.
2. 재귀함수를 타고 들어가 사이즈가 2인 경우에 방향을 탐색하면서 내부 Z를 출력합니다.
(꼭! 위 그림과 비교해서 확인하자!)
[4. 문제 풀이 코드]
/*
* @problem Z(1074)
* @url https://www.acmicpc.net/problem/1074
* @author pbg0205
*/
import java.io.*;
import java.util.*;
class Main {
static int row, col;
static int[] dx = {0, 0, 1, 1};
static int[] dy = {0, 1, 0, 1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int size = (int) Math.pow(2, n);
row = Integer.parseInt(st.nextToken());
col = Integer.parseInt(st.nextToken());
divide(0, 0, 0, size);
br.close();
}
private static void divide(int x, int y, int cnt, int size) {
if (!isBoundary(x, y, size)) {
return;
}
if (size == 2) {
for (int i = 0; i < 4; i++) {
int nx = dx[i] + x;
int ny = dy[i] + y;
if (nx == row && ny == col) {
System.out.println(cnt + i);
}
}
return;
}
int newSize = size / 2;
divide(x, y, cnt, newSize);
divide(x, y + newSize, cnt + (newSize * newSize), newSize);
divide(x + newSize, y, cnt + (newSize * newSize * 2), newSize);
divide(x + newSize, y + newSize, cnt + (newSize * newSize * 3), newSize);
}
private static boolean isBoundary(int x, int y, int size) {
return (x > row - size && x <= row) && (y > col - size && y <= col);
}
}
코드가 길어보이기만 할 뿐 내부 Z를 그려낸 코드에서 두가지 조건만 추가된 것입니다.
-
먼저 행열의 범위(isBoundary)를 벗어난 경우는 재귀함수를 탈출합니다.
-
만약 size == 2라면, 내부 Z를 그린다.
-
만약 문제에서 제시한 위치와 일치할 경우, 이동한 횟수를 출력합니다.
-
-
원하는 위치를 발견하지 못할 경우, 재귀함수를 이용해 분할 및 탐색합니다.
[5. 문제 결과]

다행히 이번에는 문제 결과가 정답이라고 나오네요;;ㅋㅋㅋ
이래서 얕은 지식이 위험합니다. 더욱 겸손히 공부하도록 하겠습니다.여기까지 Z(1074) 문제였습니다. 감사합니다!
(소스코드)
pbg0205/algorithm_study
:triumph:알고리즘 문제 풀이 저장소:triumph:. Contribute to pbg0205/algorithm_study development by creating an account on GitHub.
github.com
'Algorithm > Baekjoon' 카테고리의 다른 글
| 잃어버린 괄호 :1541번 - JAVA (0) | 2021.01.10 |
|---|---|
| 최단 경로 : 1753 - JAVA (0) | 2020.10.30 |
| 양 구출 작전 : 16437번 - JAVA (0) | 2020.10.23 |
| 트리 순회 : 1991번 - JAVA (0) | 2020.10.05 |
| 좋은 친구 : 3078번 - JAVA (0) | 2020.10.05 |




